More Examples from David McMahon’s Book, “Relativity DeMysified”
Example 2-4
Given,
the metric in plane polar coordinates, and its inverse,
and the vectors,
find
We begin,
Expanding in coordinates we have,
We also have,
So,
Now we have,
Expanding in coordinates we have,
and,
Thus,
Then,
Example 2-5
Given,
in Cartesian coordinates, show that the dot products of the basis vectors in spherical polar coordinates form the metric.
We begin with the identity,
We begin with the identity,
(1)
where we have the transformation matrix,
sometimes called the Jacobi matrix. So we have the transformations between Cartesian and spherical polar coordinates,
We now determine the basis vector transformations, using (1), expanding in components
This give us the metric component,
Then we have,
This give us the metric component,
Then we have,
This give us the metric component,
We also have the metric components,
and,
and,
This gives us the metric,





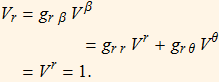






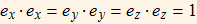

















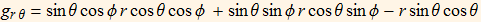
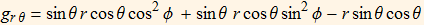






No comments:
Post a Comment