George E. Hrabovsky
James Firmiss
Example 2-3 from David McMahon’s book Relativity Demystified.
Given the line element
we seek to find the metric tensors for raising and lowering indices for vectors and one-forms. We begin by noting that the metric tensor is symmetrical,
We then identify the terms of the metric tensor. We begin with the first term,
We also have the last term,
Then we have the middle term, 2 dx dy. You might jump at this and say it is 2, but that would neglect that product of the differentials—each of which contributes half, so we have,
We can write the metric tensor,
We note that the product of the metric tensors is,
so,
We expand this term-by-term,
(1)
(2)
(3)
By (3) we get,
Rewriting (1)
or,
so,
Rewriting (2)
so,
or,
This gives us all of the components of the raised index metric tensor,
Expanding in coordinates,
Expanding this in components,


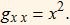








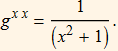













No comments:
Post a Comment